
This is Part 3 of our series, Artificial Intelligence, Poker and Regret. Our aim was to share working code of a Texas Hold’em poker AI that uses Counter Factual Regret Minimisation (CFR) and a thorough explanation of the method. What was originally envisaged as a single blog post has been drawn out by the complexity of the subject matter. As such, the three part series has been extended to 5 parts. In Part 3 we will convey the concepts behind the CFR method, using the building blocks of Regret Matching (Part 1) and Nash Equilibrium (Part 2). Part 4 will introduce a method of abstracting poker hands to deal with the combinatorial explosion of possible hands. Finally, Part 5 will bring together the abstraction of Part 4 with the CFR of Part 3 to deliver a functional Texas Hold’em poker AI.
In Parts 1 & 2, the common theme in both Rock Paper Scissors and the Prisoner’s dilemma is that each game is a single action performed by two players. Applying regret matching to single action games should be clear from Part 1, where regret refers to the difference of potential reward with actual reward. In the context of poker however, there are multiple actions of each player before any reward is given and different combinations of possible actions, resulting in many different game outcomes. Thus, a range of rewards will contribute to the calculated regret.
Let’s consider a game of five card stud poker as a traversal of the poker game tree starting from a root node that begins with the deal of five cards to all players (see animation). The betting round is an alternating sequence of actions from the players until all call or all but one fold. Note that the rewards of a particular game can be played out if we know the hands of all players, i.e. given any sequence of actions we calculate the reward, which in this case is the money in the pot. For the sake of simplicity in displaying the game tree, we consider two players and a maximum three actions to be performed before the betting round is over and cards are shown.
The challenge of applying regret matching on the larger game tree is defining the rewards (also referred to as utility) at each non-terminal node of the game tree. If we can accurately calculate a reward for each non-terminal node, then regret matching can be applied on any node as if it were a single-action game. That is, because each action would have a reward we can calculate the regret. In order to calculate the reward at a non-terminal node, we introduce the concept of the counterfactual reward. In this, counterfactual is defined as what hasn’t happened yet.
In regret matching, we not only introduced regret but also strategy, which is calculated from the accumulated positive regret. The strategy provides a probability distribution to choose the action that will minimise regret. Given that this probability distribution already reflects our tendency towards particular actions, we can also use it to reflect the future reward of that state. In particular, we can weight the future rewards of each action with the probabilities of each action to calculate the counterfactual reward for that node. In other words, the counterfactual reward is the expectation of reward using the probability distribution provided by the strategy.
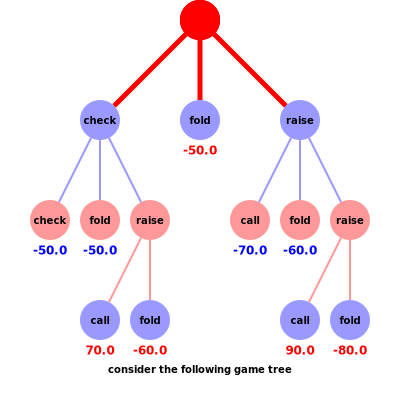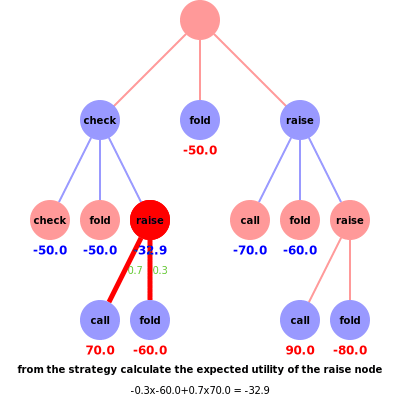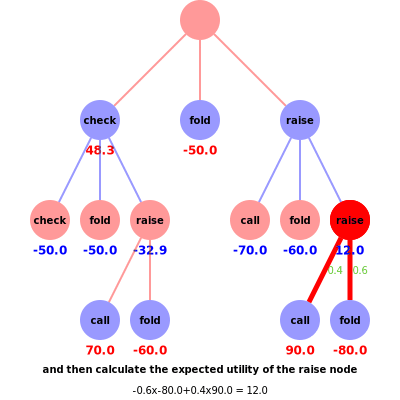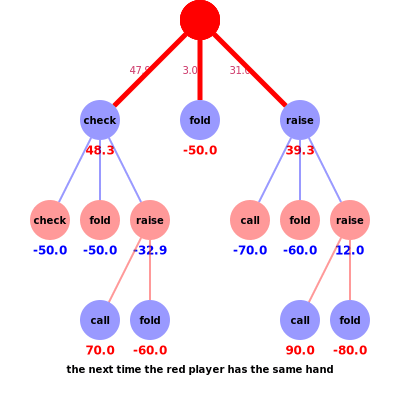
Consider the scenario in the animation, where the red player’s hand beats the blue player’s hand. Suppose the red player checked for their first action and the blue player has a final action before red calls or folds. There is a pot of $50, a bet of $10, and blue can choose to either raise, call or fold. The blue strategy (based on previous calculated regrets) dictates that blue would raise with 0.1 probability, call/check with 0.5 probability or fold with 0.4 probability. The corresponding rewards are check = -50, fold = -50 or raise = ??, which awaits red’s final action. The counterfactual reward for blue, i.e. the first check node, is ?? x 0.1 + -50 x 0.5 + -50 x 0.4 = ?? x 0.1 + -45. To calculate the reward for ??, we consider red’s strategy where, based on previous regrets, the probabilities of red calling =0.7 and folding =0.3 allow us to calculate the counterfactual reward for red, i.e. the raise node on the left branch, -?? = 0.7 x 70 + 0.3 x -60 = 32.9. Note the colours of the utilities in the animation represent the utility for the corresponding player, i.e. if red wins blue loses and vice versa. Thus the counterfactual reward for blue’s last action is -32.9 x 0.1 + -45 = -48.3, which again defines the counterfactual reward for red’s initial check action to be 48.3.
So above shows how regret matching can still be applied to multi action games to give rise to the CFR method. We showed in part 2 that regret matching helps us to determine the Nash Equilibrium, and conveniently, the same argument still holds in the context of multi action games, In particular, the average strategy approximates to a Nash Equilibrium, so long as the overall regret is significantly small (Theorem 2).
Because of the multiple actions in poker, however, both the average strategy and regret calculations are weighted by the opponents’ strategies. The reasons for this are to ensure that the accumulated regret and average strategy don’t grow out of control for future actions. This is not portrayed in the animation but is conveyed in the code with the passing of both players’ strategies through the recursive function.
To summarise, in regret matching we use strategy to choose an action but in CFR, strategy also plays a role in calculating the reward and thus the regret. In CFR, the strategy is also important in calculating the average strategy which approaches the Nash Equilibrium.
With respect to limit five card stud poker, our implementation of CFR would theoretically reach this equilibrium after some large computation time and playing of millions of games but due to the large number of combinations of cards, convergence would take an unnecessary long time. With this explosion of possible hands, we are forced to abstract the poker hands in order to have a smaller state space and thus reduce the computation time.
This method of abstraction we will introduce in Part 4 of this poker AI series.
Shahrad Jamshidi
Lead Researcher
Remi AI
Stay tuned on the Remi AI blog as we build out the complete supply chain offering!
Or, if you're ready to start seeing the benefits of A.I-powered inventory management, start the journey here.
Who are we?
Remi AI is an Artificial Intelligence Research Firm with offices in Sydney and San Francisco. We have delivered inventory and supply chain projects across FMCG, automotive, industrial and corporate supply and more.
Want to know more? Sign up to our newsletter for the latest information from us and other knowledgeable folk in the market.